はい.どらびです.
今回は前回のこちら

に引き続き,車やバイクの構造変更届にかかわる強度計算についてお話します.
この記事書いてるモチベは主に3つあって,
- 父から参考としてもらった資料の計算の説明があまりにも足りず意味不明&下手したら間違っている説がある.
- 単純に詳しい資料が少なく,とっつきづらい.
- 高校や大学で学ぶ計算が,こんなところでも活かせるんだよーっていう実例を示したい.
ということで,ここでは単純に強度計算に必要な式(の一例)を,実際の計算例を交えて紹介する他,なぜこの式が出てくるのかと,その式についての大まかな説明を入れていきます.
今回は,フロントおよびリアスプロケット,チェーンの交換に際する強度計算の例を示します.
ではでは始めましょう.
スプロケットの強度計算
ということでまずはスプロケットの計算から始めます.
チェーンにかかる引っ張り荷重の計算
一番最初に,カウンターシャフトにかかる最大トルクを計算します.基本的にはこれがフロント(ドライブ)スプロケットにかかり,チェーンを通じてリアスプロケットに…という形で,全ての駆動系にかかる力の計算の元になります.
$$T_{max}=T \times i_0 \times i_1 =(11.8 \times 1.84 \times 2.294 = 49.7 kgf \cdot m)$$
式中の記号をそれぞれ説明すると,$T_max$はカウンターシャフトにかかる最大トルク,$T$はバイク諸元に記載されているエンジンの最大トルク,$i_0$,$i_1$はそれぞれ1次,2次の減速比になります.スプロケットを交換していなければ,全てバイクor車のユーザーマニュアルに記載があると思います.
次,そこからチェーンにかかる最大の引っ張り荷重は以下の様に計算できます.
$$T_0=\frac{T_{max}}{\frac{1}{2} D_s} \times 10^3=(1151kg)$$
$D_s$はスプロケットのピッチ円径です.
計算された最大荷重がチェーンの破断荷重に対して十分な強度を持っているかどうかを計算します.安全係数は,1.6以上あれば日本での車検は通ります.ちなみにほかの部分でより厳しい条件が科される場合が多いので,ここで引っかかることはそうそうないと思います.ちなみに今回私が計算した最大荷重に対してチェーンの破断荷重は3.28倍ありました.
ドライブスプロケットにかかる応力の計算
次はドライブスプロケットにかかる応力を計算していきます.
スプライン部の圧縮応力
歯面に作用する力は,トルクを用いて次のように計算できます.(下記サイト:歯面強さより)
$$P=\frac{T_q}{\eta HLZd_p}=(\frac{49.7 \times 10^3}{1.0 \times (2.0 \times 1.667) \times 13 \times (13 \times 1.667)} = 52.914)$$
ここで,それぞれの数字,記号の意味は,
$T_q$は歯面にかかるトルクを表し,最大値が知りたいのでここでは先ほどの$T_{nax}$をそのまま利用します.ただし単位を合わせるために1000がかけられていることに注意です. $\eta$は噛み合い率,$H$は噛み合い歯丈,$L$は噛み合い長さ,$Z$は歯数,$d_p$はピッチ円直径です.
今回の例では,スプラインの材質はSCM435であり,許容圧縮応力は94.834 kgf/mm^2であるから,破壊安全率は,$94.834/52.914=1.792>1.6$と計算できるので,基準を満たしていることがわかります.
スプロケット歯面の最大応力
スプロケットの歯面にかかる応力の計算は結構複雑になります.
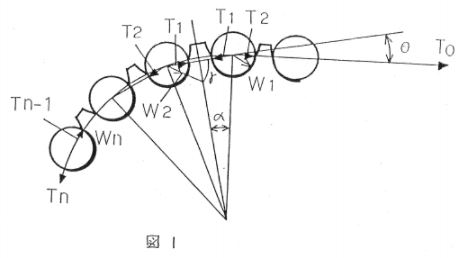
図のように,スプロケットの歯面とチェーンの接触を考えて,歯面にかかる最大の接触力をまずは算出します.図1より,
$$\frac{T}{\sin(x – (\gamma + 2\alpha))} = \frac{T}{\sin(\gamma + 2\alpha – \theta)} … (1)$$
$$\frac{T_n – 1}{\sin(x-(\gamma + 2\alpha))} = \frac{T_n}{\sin\gamma} … (2)$$
$$T_n = T_0 (\frac{\sin\gamma}{\sin(\gamma+2\alpha)})^{n-1} \cdot \frac{\sin(\gamma+2\alpha-\theta)}{\sin(\gamma+2\alpha)} … (3)$$
さらに$W_n$の付近の力とトルクにのみ注目したのが図2で,角度と歯数との兼ね合わせから以下の様に歯面にかかる力を導出できます.
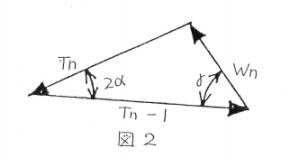
$$W_n = \sqrt{T^{2}_{n} + T^{2}_{n-1} -2T_n\cdot T_{n-1}\cos2\alpha}$$
ここで,図1,2から角度を導出すると,
$$\alpha = 180/Z = 180/17 = 10.588^\circ$$
$$\gamma = 35 – 120/Z = 27.941^\circ$$
$$ T_0 = T_{max} = 1151 kgf$$
$$ \theta = 10.588^\circ$$
となるので,Wの最大値は
$$W_{max} = 279.732$$
と計算できます.(数値代入は省略します.)
次に,この接触力が歯面にどのように加わるのかを考えます.これはヘルツの接触応力の公式というものがあって,接触する二つの物体の形状に応じて異なる式がありますが,ギアとチェーンの噛み合いについては図3のように円柱と凹円筒面の接触が該当します.
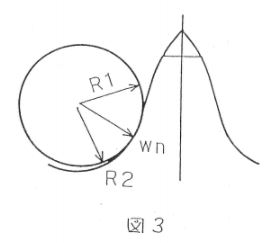
これに関する接触応力の公式である,以下の1式だけ覚えておけば大丈夫だと思います.
$$P_n = 0.418 \times \sqrt{\frac{R_2 – R_1}{R_1 R_2} \times \frac{W_n}{b} \times \frac{E_1 E_2}{E_1 + E_2}}$$
まあ難しいんですけどね…
で,この式を実際に今回の例に適用するとこんな感じになります.
$$ P_n = 0.418 \times \sqrt{\frac{5.21 – 5.15}{5.15 \times 5.21} \times \frac{279.732}{7.9} \times \frac{21617.2122}{2}} = 12.6$$
詳しくは以下の資料を参考にしてみてください.
http://www.mekatoro.net/digianaecatalog/tsubaki-drivech/book/tsubaki-drivech-P0137.pdf
で,最大接触力は求められました.スプロケット材料の許容圧縮応力は$94.834 kg/mm^2$ですので,明らかに安全率の条件を満たしています.
スプロケット歯にかかる最大曲げ応力
次は曲げ応力になります.何が違うんじゃい,と思うかもしれませんが,簡単に説明すると,
先ほど計算したのが「歯面が押しつぶされる力で変形しないか」,
これから計算するのが「歯が欠けないか,折れないか」
と考えてもらえればOKかなと思います.この際理屈がわからなかったとしても,どちらの計算も必要になることは確定してますので,あきらめて両方計算してください.
また図を使って説明していきます.
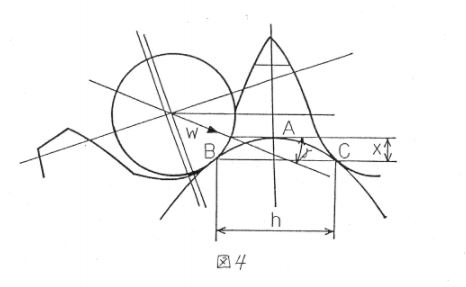
図4より,A点を通り,スプロケット歯面に接する放物線の接点B,Cを求め,x,bの値を求めると,次のようになります.(B,C点で最大曲げ応力が生じる.)
$$\gamma = 27.941$$
$$d = 1.52\sqrt{\frac{W_1}{b}\frac{E_1 + E_2}{E_1 E_2}\frac{R_1 R_2}{R_2 – R_1}} = 1.785$$
$$h = 1.4R_1 + 2d\sin\gamma = 1.4 \times 5.15 + 2 \times 0.837 = 8.884$$
$$x = d\cos\gamma = 1.577$$
この式から,
$$Z_1 = \frac{1}{6}bh^2 = 103.919$$
$$M = W\cos\gamma \times x = 279.732 \times 0.88343 \times 1.577 = 389.714$$
$$\delta_{max} = \frac{M}{Z_1} = 3.750$$
と計算されます.
結果から,安全率を満たしているかを再度計算します.
材料の曲げ強さは許容圧縮応力の2/3が目安とされるので,安全率は
$$\frac{94.834 \times 2}{3.750 \times 3} = 16.859 > 1.6$$
となっているので,今回の例は基準を満たしていることがわかります.
リアスプロケットにかかる応力の計算
基本的には上のドライブスプロケットにかかる応力の計算と利用する式は
同じで,歯数等,式の中の数値が変更になるだけです.ということでここでは計算例のみ載せます.先の例で意味が分かった,という方はこの節は飛ばしてもらって構いません.
スプライン部の圧縮応力
リアスプロケットはスプライン接続ではなくボルトによる接続のため当該計算は必要ありません.ということで飛ばします.
計算書にはなぜ計算が必要ないのか,上のような文を一筆書いておくと差し戻しなどのリスクを減らせると思います.
スプロケット歯面の最大接触応力
$$\alpha = \frac{180}{43} = 4.186^\circ$$
$$\gamma = 35 – \frac{120}{43} = 32.209^\circ$$
$$T_0 = 1151 kgf$$
$$\theta = 4.186^\circ$$
$$T_n = T_0 \frac{\sin(\gamma + 2\alpha – \theta)}{\sin(\gamma + 2\alpha)} = 1151 \times \frac{0.593}{0.659} = 1035.725$$
$$W_1 = \sqrt{948.313^2 + 1151^2 – 2 \times 948.313 \times 1151 \times \cos(10.588^\circ)} = 140.174$$
ポアソン比0.30で凹円柱面の接触なので
$$P_n = 0.418 \times \sqrt{\frac{R_2 – R_1}{R_1 R_2} \times \frac{W_n}{b} \times \frac{E_1 E_2}{E_1 + E_2}} $$
$$= 0.418 \times \sqrt{\frac{5.21 – 5.15}{5.21 \times 5.15} \times \frac{140.174}{7.9} \times \frac{21000 7300}{21000 + 7300}} = 6.3$$
材料の許容圧縮応力は$58.124 kgf/mm^2$で,安全率は$68.124/6.3 = 9.226 > 1.6$となり,条件を満たす.
スプロケット歯にかかる最大曲げ応力
各部寸法計算(図4の)
$$\gamma = 32.209$$
$$d = 1.52\sqrt{\frac{W_1}{b}\frac{E_1 + E_2}{E_1 E_2}\frac{R_1 R_2}{R_2 – R_1}} = 1.785$$
$$h = 1.4R_1 +2d\sin\gamma = 1.4 \times 5.15 + 2 \times 0.837 = 8.884$$
$$x = d\cos\gamma = 1.577$$
したがって,
$$Z_1 = \frac{1}{6}bh^2 = 103.919$$
$$M = W\cos\gamma \times x = 140174 \times 0.88343 \times 1.577 = 195.286$$
$$\delta_{max} = \frac{M}{Z_1} = 1.879$$
材料の曲げ強さは許容圧縮応力の2/3が目安とされるので,安全率は,$58.124 \times 2 / 1.879 \times 3 = 20.622 > 1.6$で条件を満たします.
まとめ
ここまでで,改造申請に必要な計算の内,スプロケットに関わる部分の計算が完了しました.
スプロケットやチェーンを純正品以外のもの,特に強度が弱まる方向に変更した場合はこの手の計算が必要になると思います.
次は,ギアボックスの計算例を掲載予定です,ただしここまでの改造をしている人は本当に少数だと思いますので,どこまでお役に立つかは不明です…
ではまた.



コメント